Essentials
Essentials
References:
Essential Mathematics for Computational Design
Points, vectors and planes
Points, vectors and planes are the base for creating and transforming geometry in Grasshopper.
Points
Points in 3D space have three coordinates, usually referred to as [x,y,z]. Points in 2D space have only two coordinates which are either called [x,y] or [u,v] depending on what kind of two dimensional space we’re talking about.
2D Point
\[\dot{P}= \left[\begin{matrix}x\\y\\\end{matrix}\right]\] \[\dot{P}= \left[\begin{matrix}2\\3\\\end{matrix}\right]\]pt2d = [2,3]
3D Point
\[\dot{P}= \left[\begin{matrix}2\\3\\3\\\end{matrix}\right]\]pt3d = [2,3,3]
Vectors
A vector is a geometric quantity describing Direction and Magnitude. Vectors are abstract.
2D vector
\[\overrightarrow{v}= \left[\begin{matrix}v_1\\v_2\\\end{matrix}\right]\] \[\overrightarrow{v}= \left[\begin{matrix}2\\3\\\end{matrix}\right]\]vec2d = [2,3]
3D vector
\[\overrightarrow{v}= \left[\begin{matrix}v_1\\v_2\\v_3\\\end{matrix}\right]\]vec3d = [2,3,3]
ie. they represent a quantity, not a geometrical element.
Vector and points are both lists of three numbers so there’s absolutely no way of telling whether a certain list represents a point or a vector. A vector is an arrow in space which always starts at the world origin (0.0, 0.0, 0.0) and ends at the specified coordinate.
Dot product
Known as the “scalar product”, is an operation that takes two vectors A and B, and returns a scalar quantity (number). The dot product of two vectors can be defined as the product of the magnitudes of the two vectors and the cosine of the angle between the two vectors. Alternatively, it is defined as the product of the projection of the first vector onto the second vector and the magnitude of the second vector.
\[A \cdot B = |A| |B| cos (\alpha)\]Cross product
Operation on two vectors in three-dimensional space. Given two linearly independent vectors A and B, the cross product, is a vector that is perpendicular to both and normal to the plane containing them. It should not be confused with the dot product (projection product).
\[A \times B = |A| |B| sin (\alpha)\]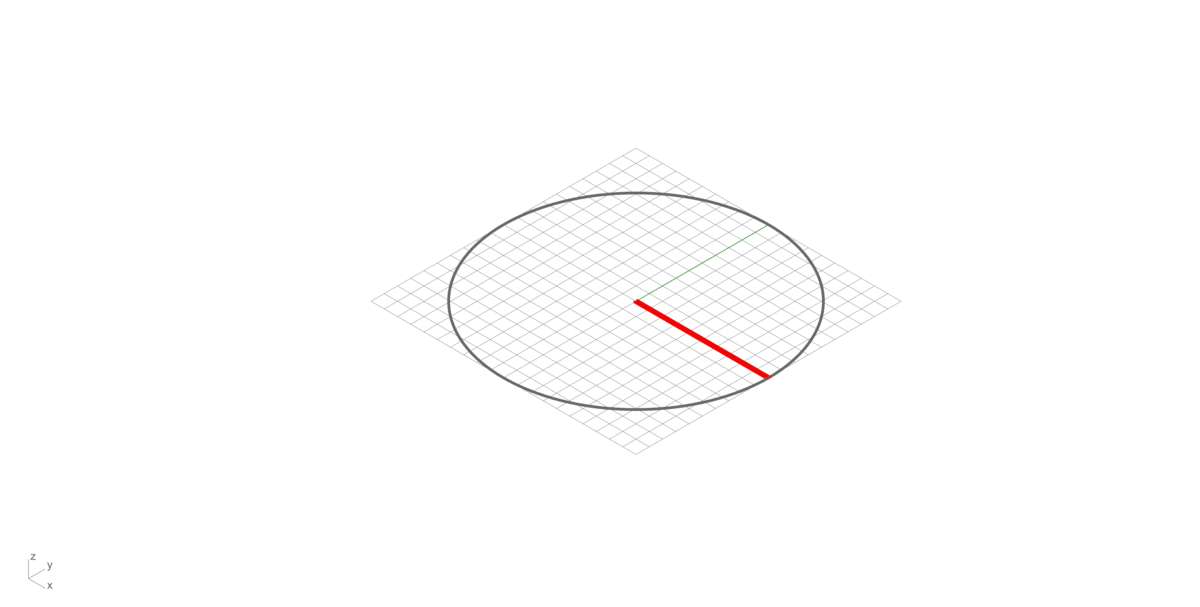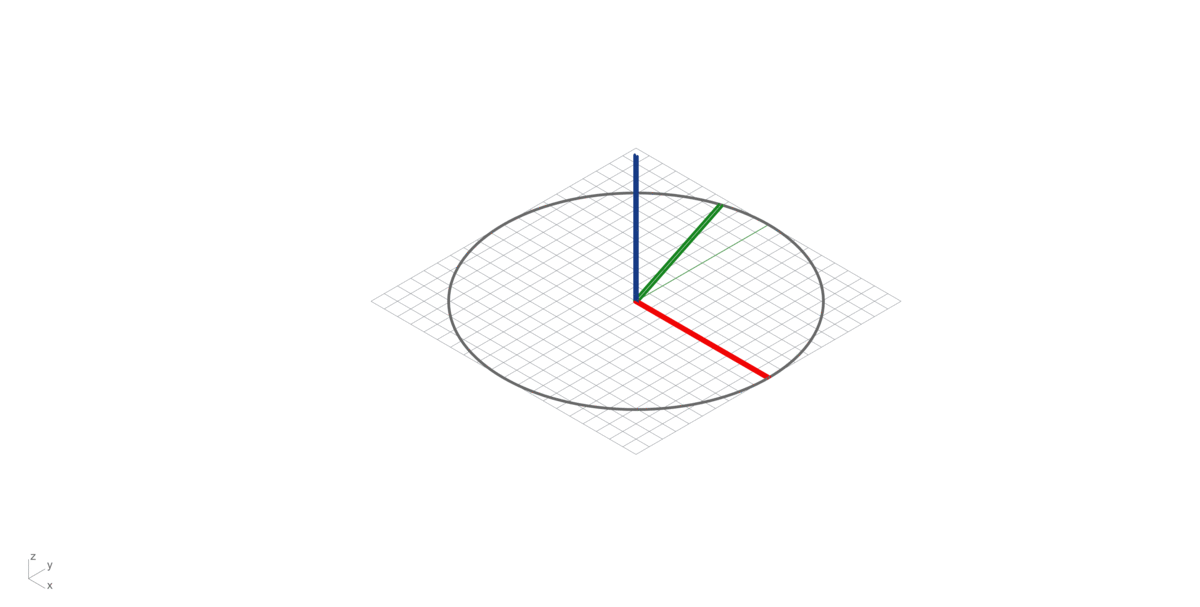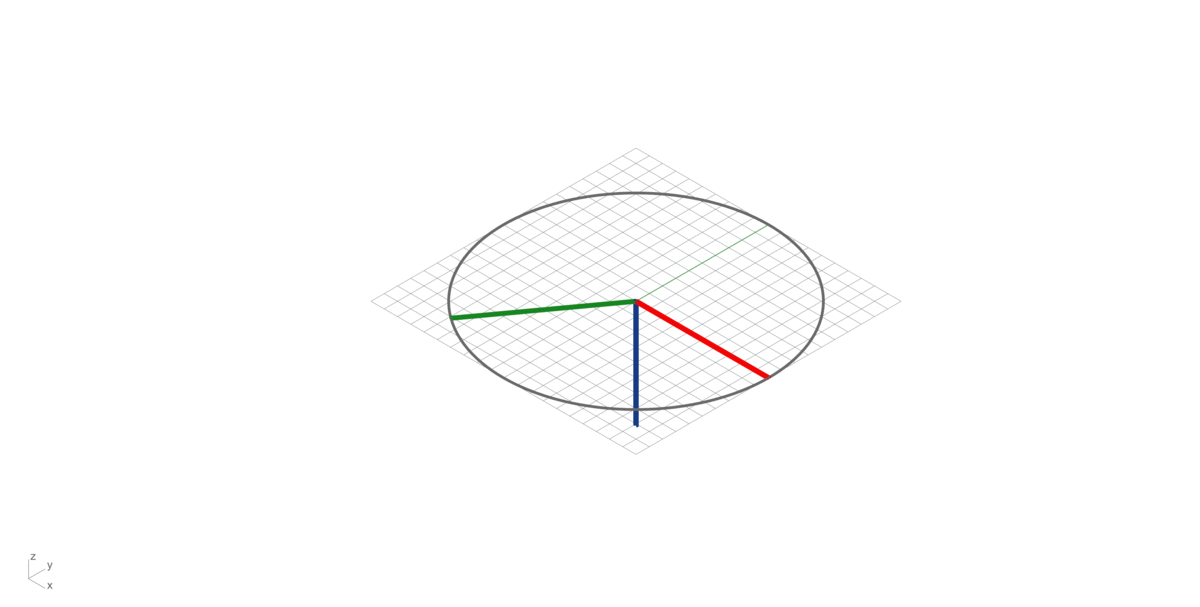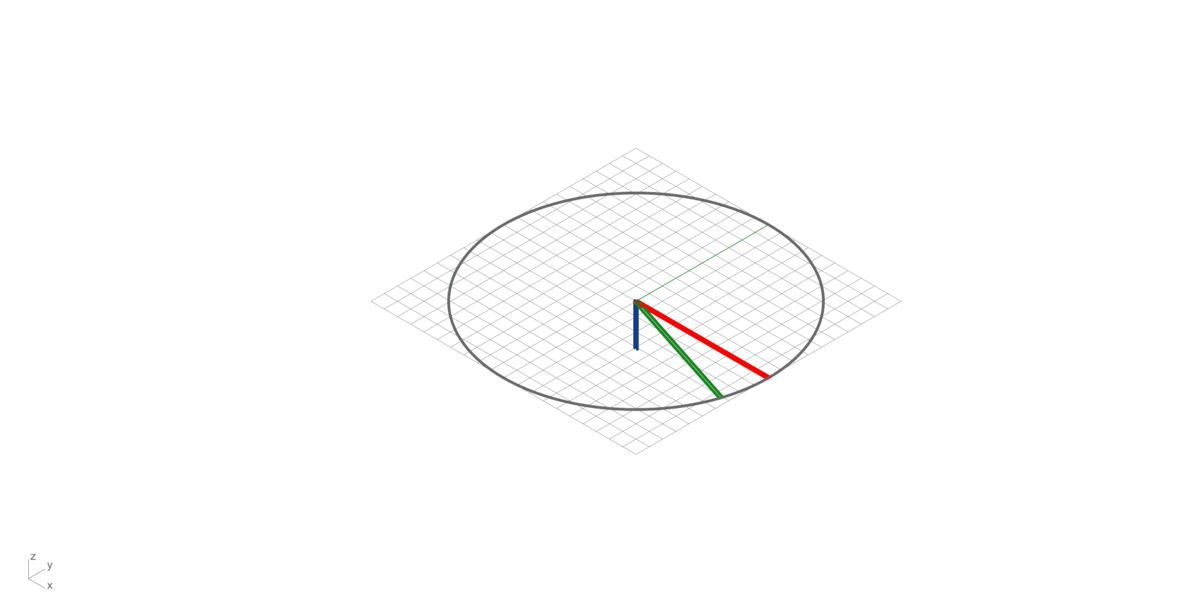
Right hand rule in vector multiplication
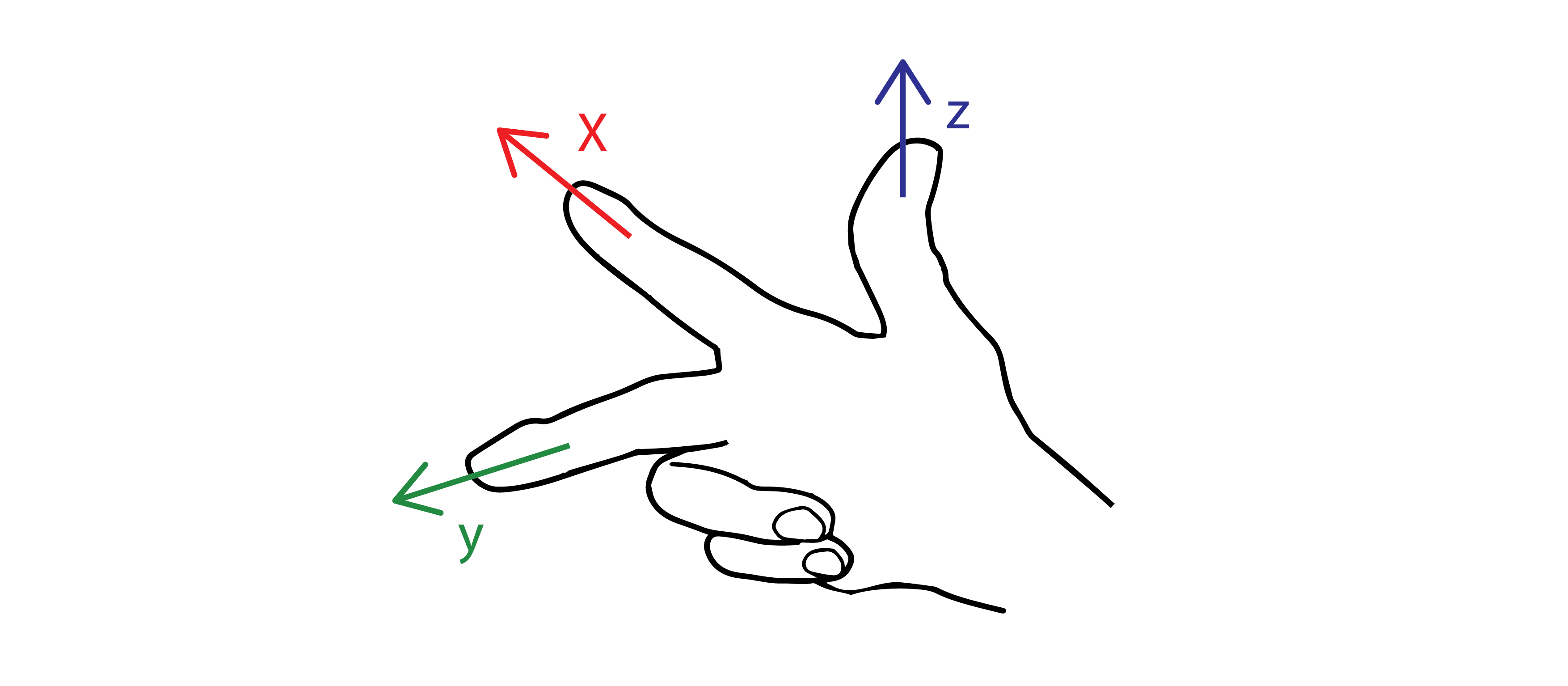
Planes
Planes are “Flat” and extend infinitely in two directions, defining a local coordinate system.
Basics Maths
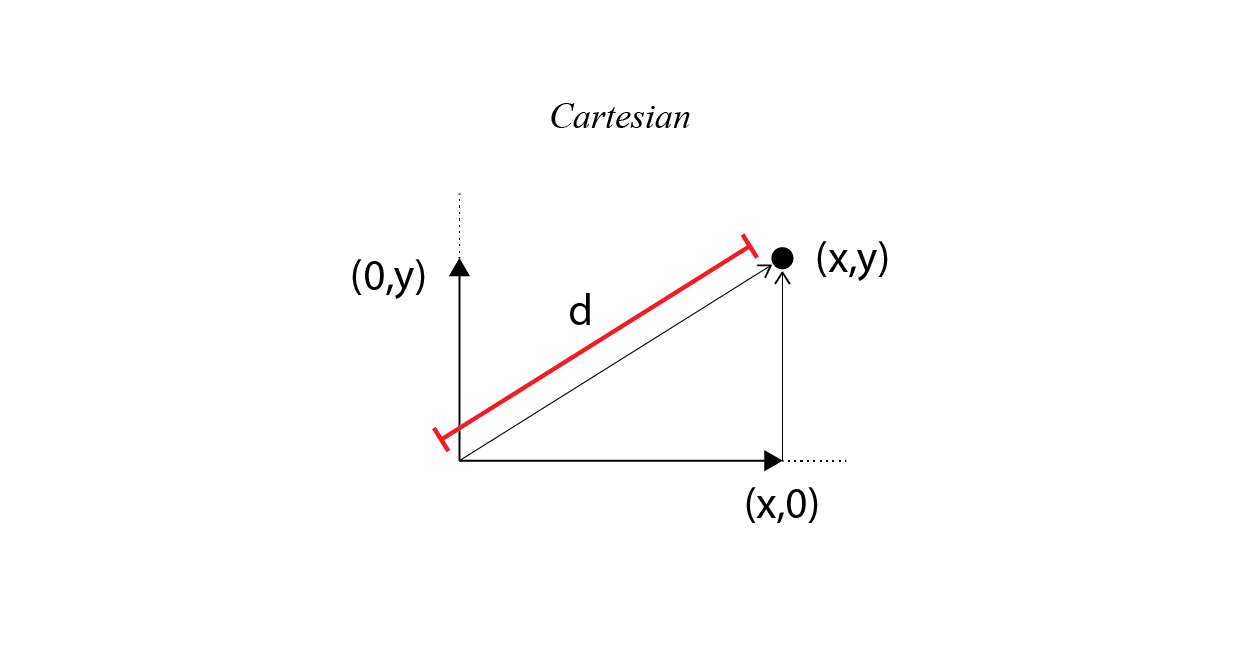
Cartesian coordinate system
Specifies each point uniquely in a plane by a set of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length.
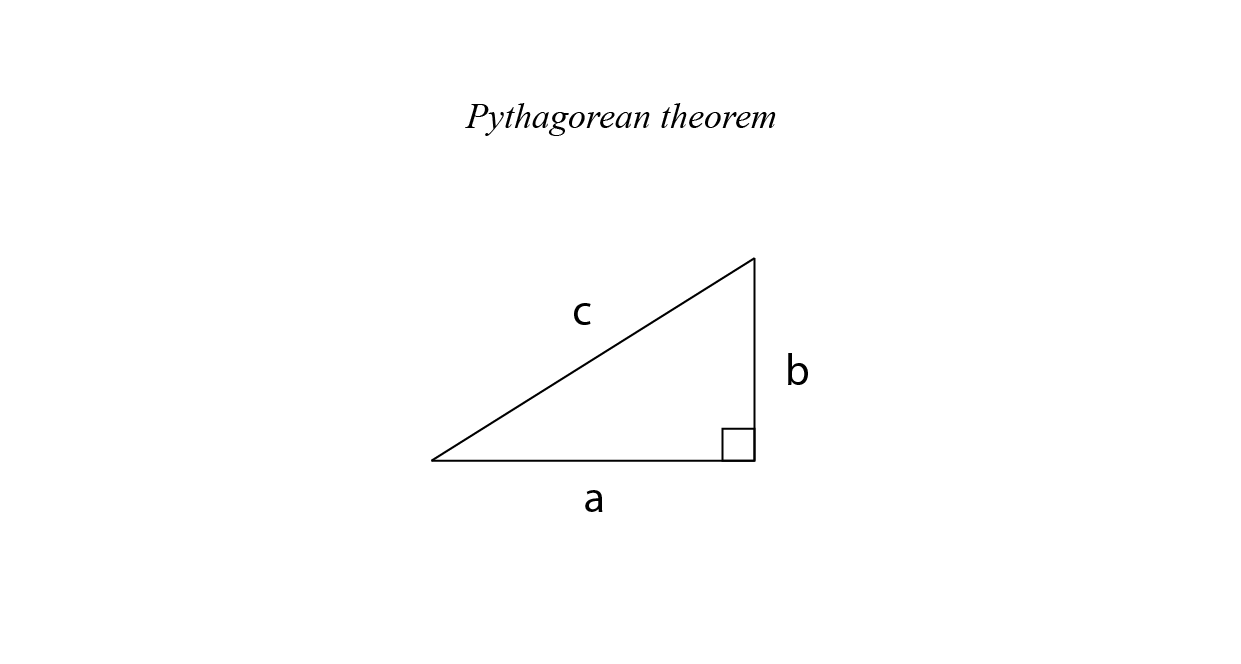
Pythagorean theorem
Is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides a, b and c, often called the “Pythagorean equation”
2D Functions
Change the functions by different values or substitute them by other equations.
//Examples:
y = sin (x)
y = cos (x)
y = tan(x)
//...etc
Graphing by FredieRa
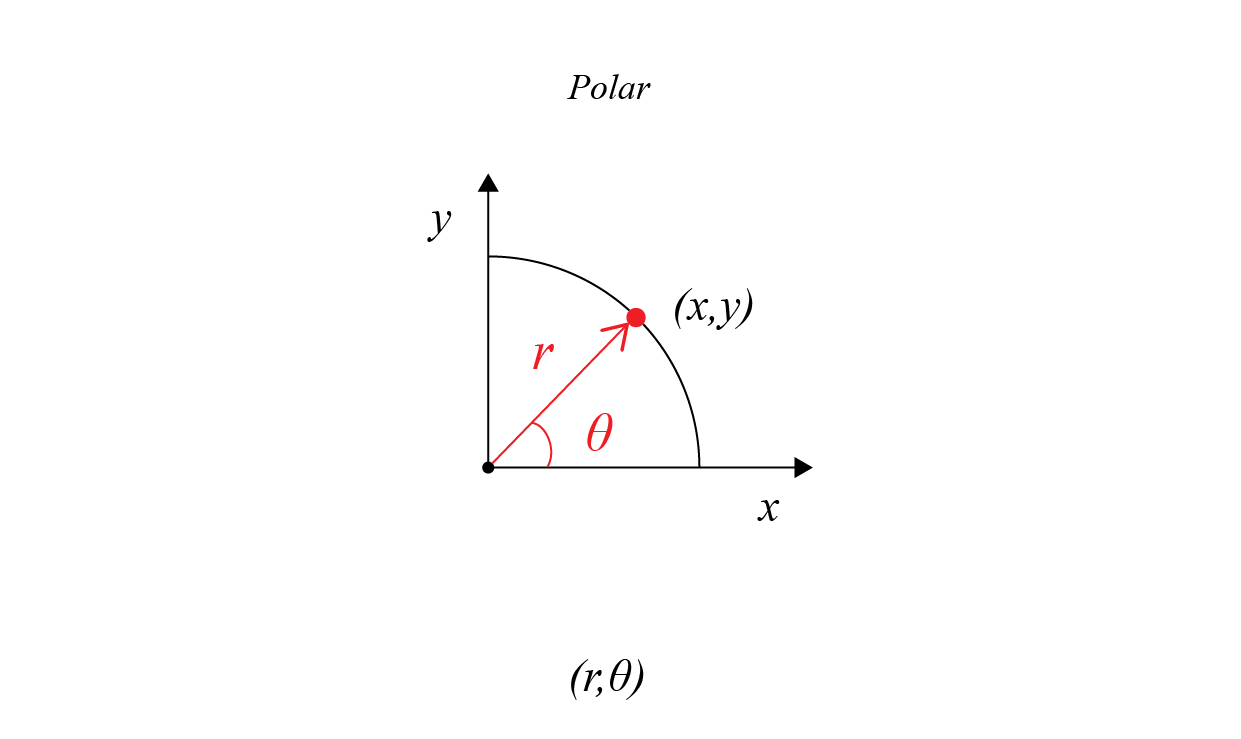
Polar coordinate system
Is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point (analogous to the origin of a Cartesian coordinate system) is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth. The radial coordinate is often denoted by r or ρ, and the angular coordinate by φ, θ, or t.
Angles in polar notation are generally expressed in either degrees or radians (2π rad being equal to 360°).
Polar to cartesian
The polar coordinates r and θ can be converted to the Cartesian coordinates x and y by using the trigonometric functions sine and cosine:
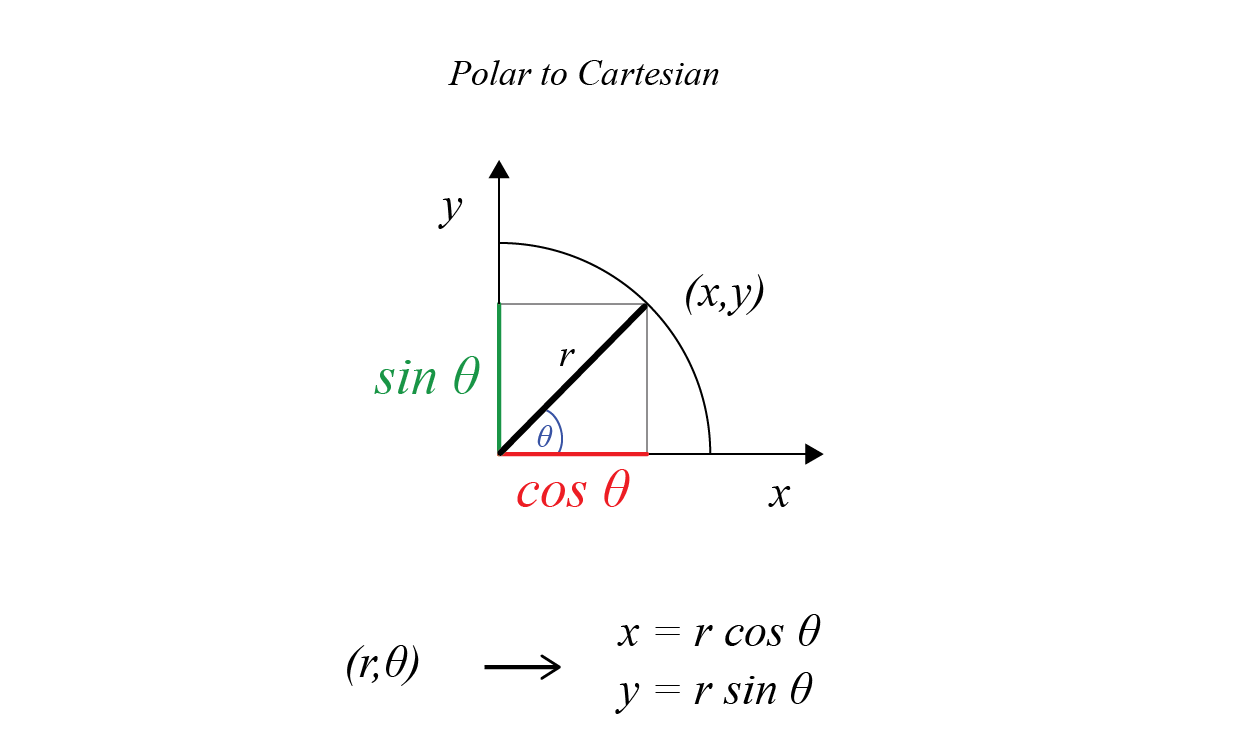
Polar mapping
x = r * cos(i)
y = r * sin(i)
Instructions: RIGHT = Next pattern, LEFT = Prev pattern, UP = Next “interesting” pattern, DOWN = Prev “interesting” pattern, SPACE = Pause, P = Toggle “marked” cube to prove it’s just going in a circle.
Degrees vs. Radians
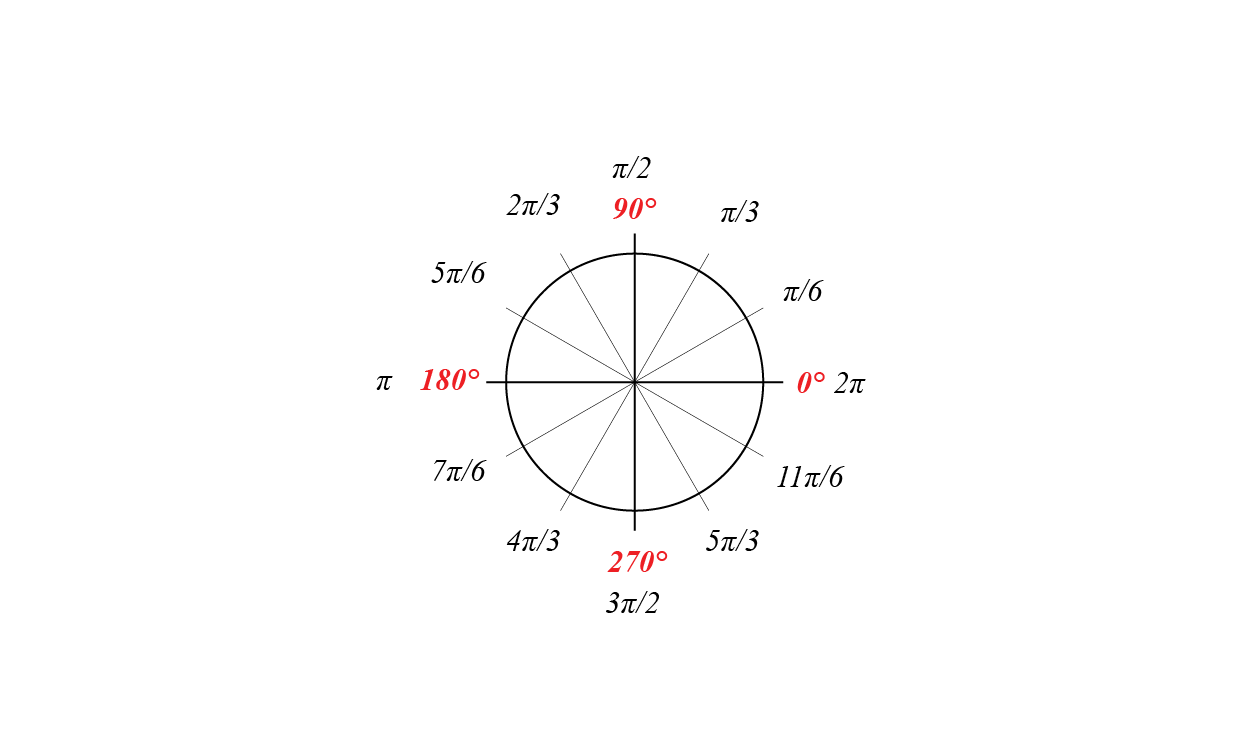
| Sin | Cos |
|---|---|
| sin(0) = 0 ; | cos(0) = 1 |
| sin(90) = 1 | cos(90) = 0 |
| sin(180) = 0 | cos (180) = 1 |
| sin(270) = -1 | cos (270) = 0 |
| sin(360) = 0 | cos (360) = 1 |
Cylindrical coordinate system
Is a three-dimensional coordinate system that specifies point positions by the distance from a chosen reference axis, the direction from the axis relative to a chosen reference direction, and the distance from a chosen reference plane perpendicular to the axis.
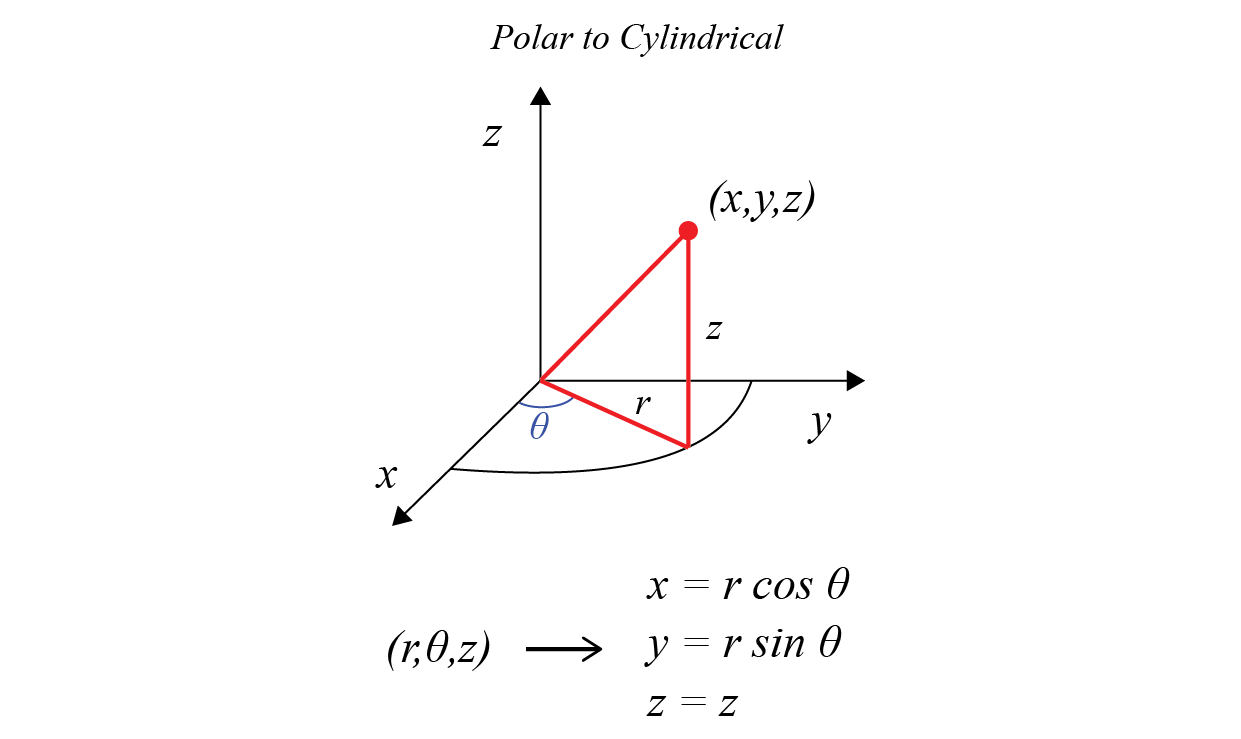
Cylindrical mapping
x = r * cos(i)
y = r * sin(i)
z = i
Instructions: RIGHT = Next pattern, LEFT = Prev pattern, UP = Next “interesting” pattern, DOWN = Prev “interesting” pattern, SPACE = Pause, P = Toggle “marked” cube to prove it’s just going in a circle.
Graphing by FredieRa
Spherical coordinate system
Is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its polar angle measured from a fixed zenith direction, and the azimuthal angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane. It can be seen as the three-dimensional version of the polar coordinate system.
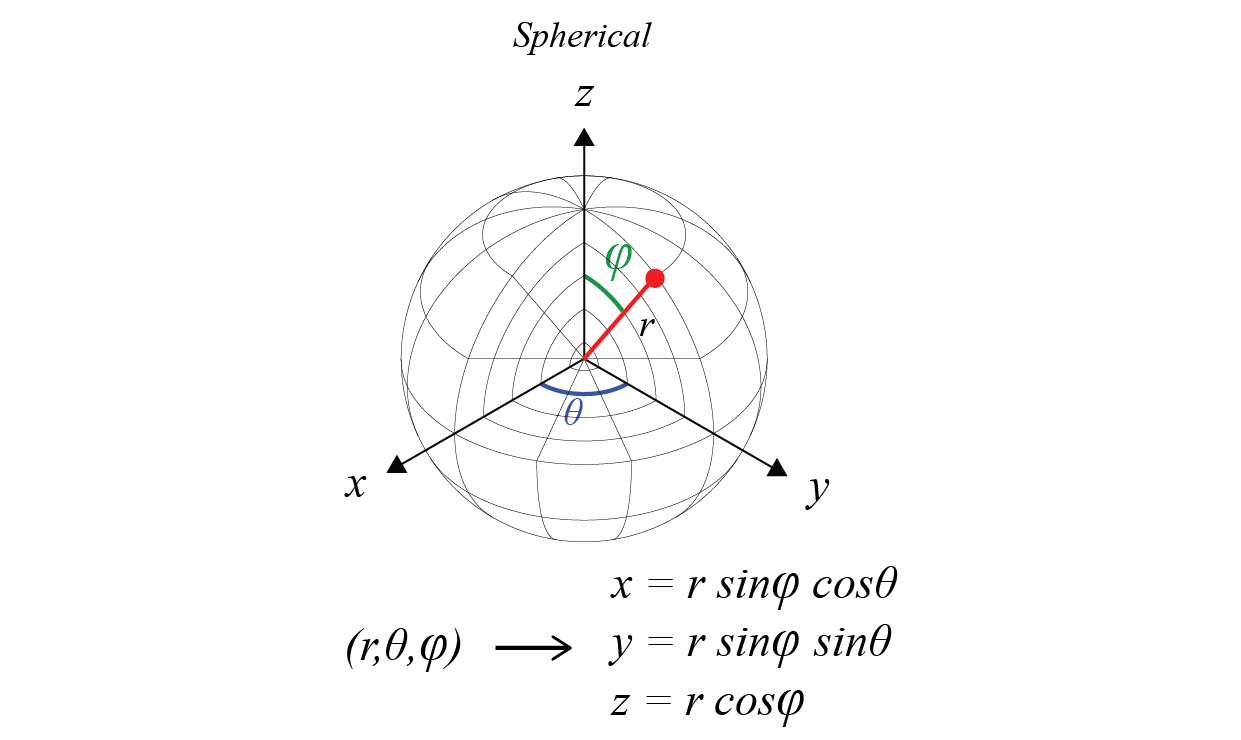
Spherical mapping
x = r * (sin(i)) * (cos(j))
y = r * (sin(i)) * (sin(j))
z = r * (cos(i))
Instructions: RIGHT = Next pattern, LEFT = Prev pattern, UP = Next “interesting” pattern, DOWN = Prev “interesting” pattern, SPACE = Pause, P = Toggle “marked” cube to prove it’s just going in a circle.
Graphing by FredieRa







