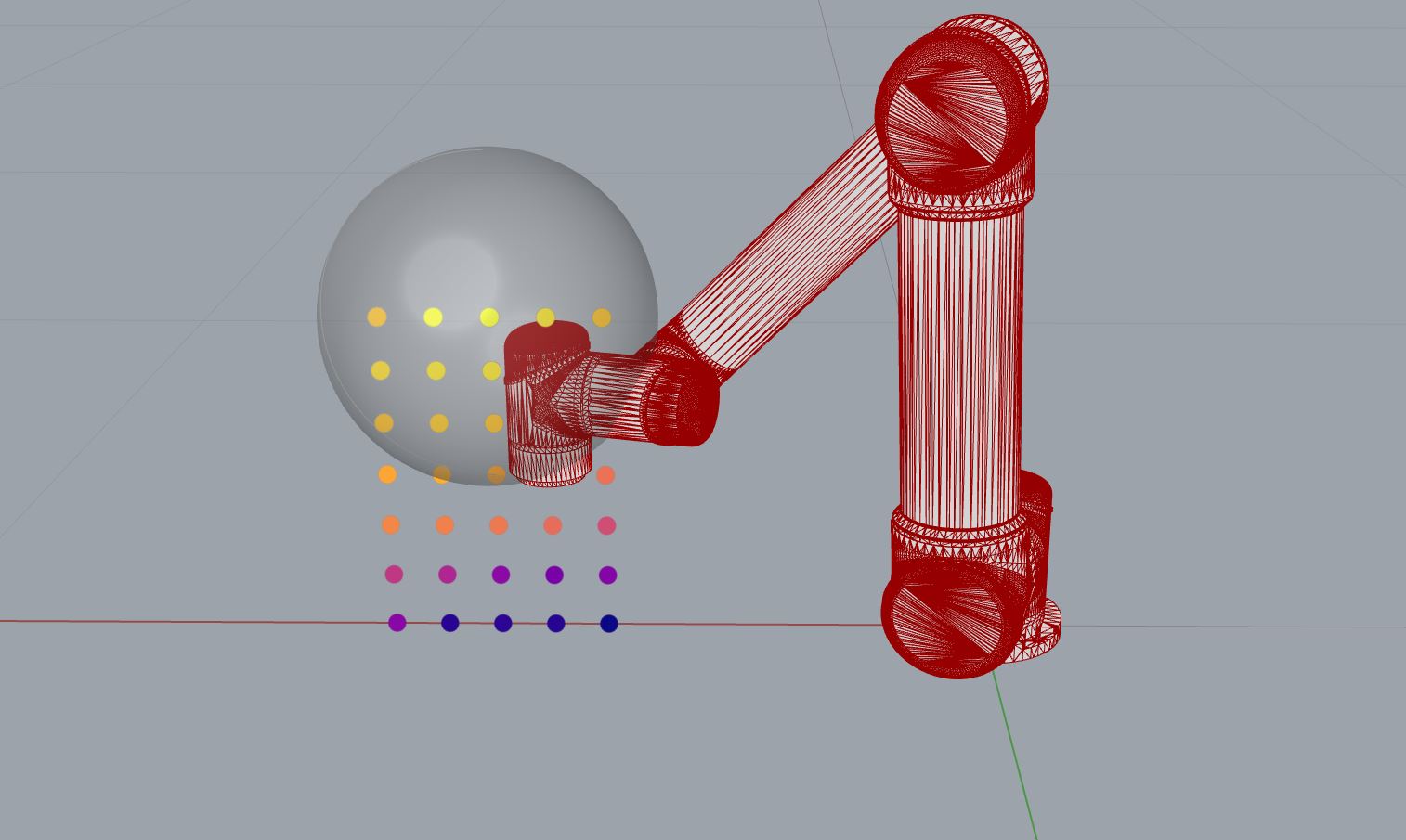
Reachability Map 2D
The example in the introduction used a list of frames on specific points on the sphere to calculate the reachability map (1D). For the next two examples, we want to generate a list of a list of frames and use these for the calculation (2D).
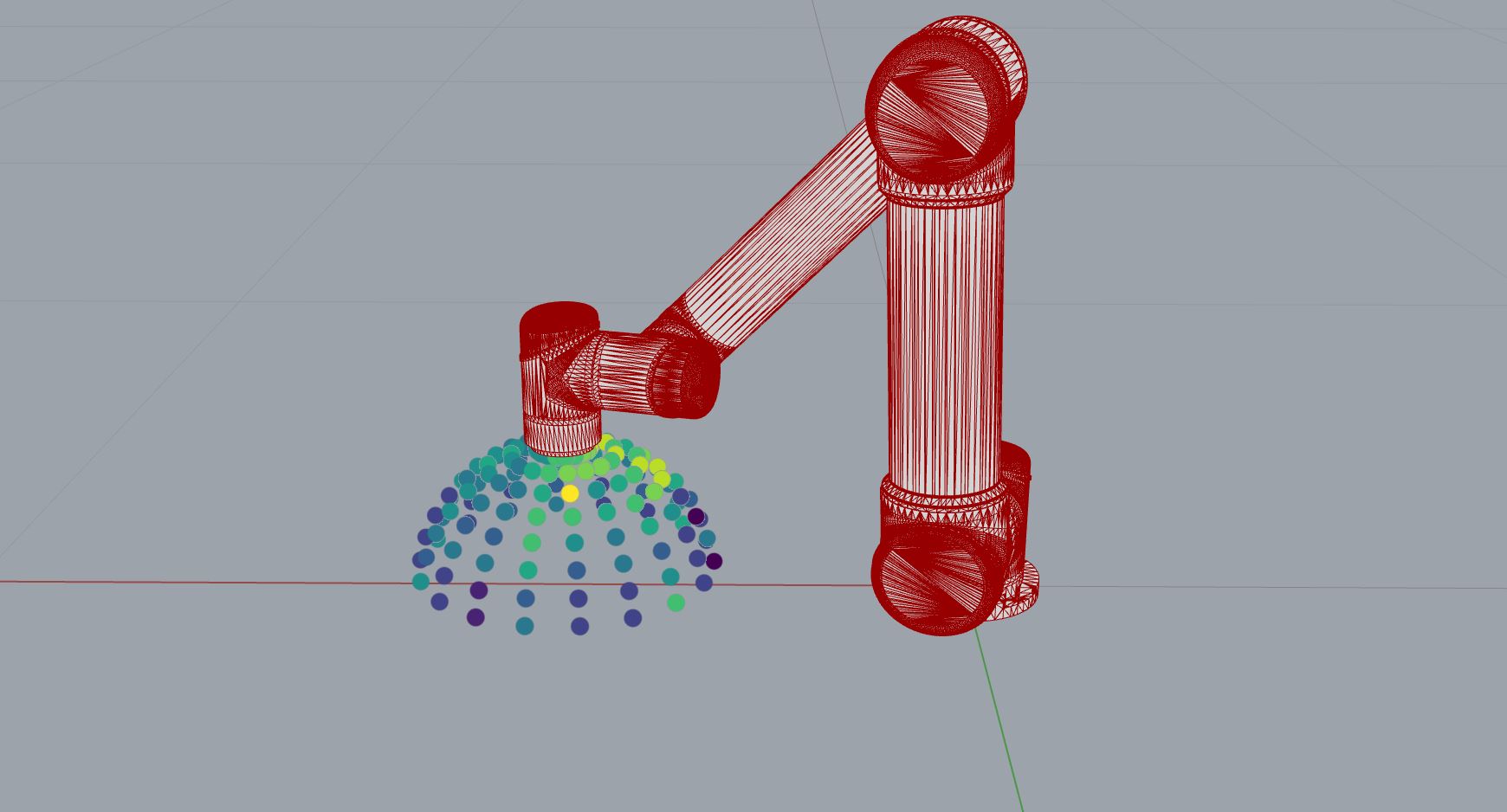
Example 02: reachability map 2D with deviation vectors
Additionally to the points_on_sphere_generator from Example 01, we create a
deviation_vector_generator.
import math
from compas.geometry import Frame
from compas_fab.robots import DeviationVectorsGenerator
def deviation_vector_generator(frame):
for xaxis in DeviationVectorsGenerator(frame.xaxis, math.radians(40), 1):
yaxis = frame.zaxis.cross(xaxis)
yield Frame(frame.point, xaxis, yaxis)
And combine both generators into a generator that yields a list of a list of frames (2D).
def generator():
for frame in points_on_sphere_generator(sphere):
yield deviation_vector_generator(frame)
The robot is set up as in Example 01 and we calculate the reachability map as follows.
>>> map = ReachabilityMap()
>>> map.calculate(generator(), robot, options)
>>> map.to_json(os.path.join(DATA, "reachability", "map2D_deviation.json"))
The visualization of the results in Rhino/GH looks different than in Example 01, as the scores per evaluated point are now more scattered and range between 16 (dark purple) and 26 (yellow).
Example 03: reachability map 2D with sphere points
In this example, we want to know the best reachable sphere from Example 01. Therefore, we create a sphere generator:
from compas.geometry import Sphere
from compas.geometry import Vector
def sphere_generator():
sphere = Sphere((0.35, 0, 0), 0.15)
for x in range(5):
for z in range(7):
center = sphere.point + Vector(x, 0, z) * 0.05
yield Sphere(center, sphere.radius)
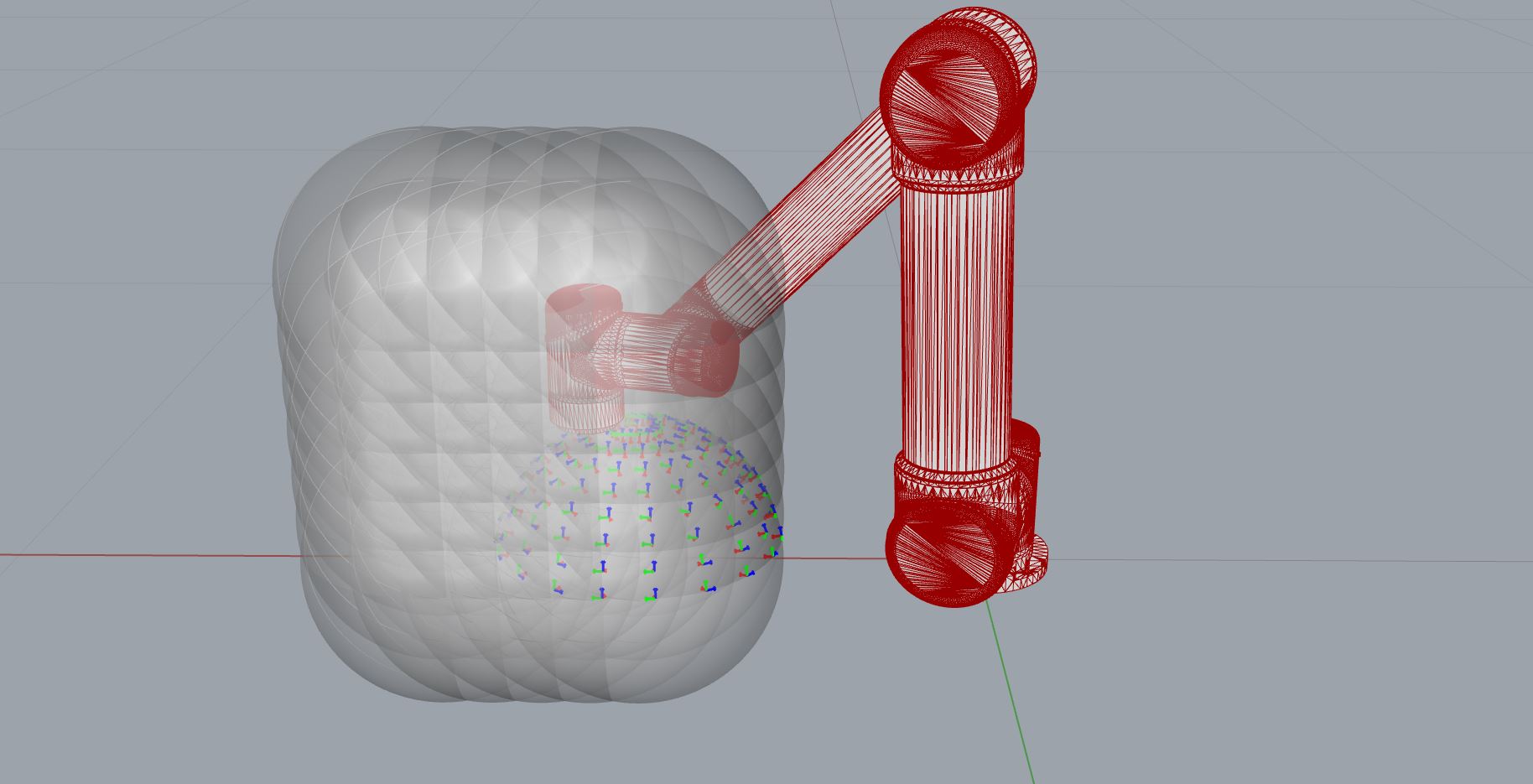
And use it together with the points_on_sphere_generator to create a 2D frame generator.
def generator():
for sphere in sphere_generator():
yield points_on_sphere_generator(sphere)
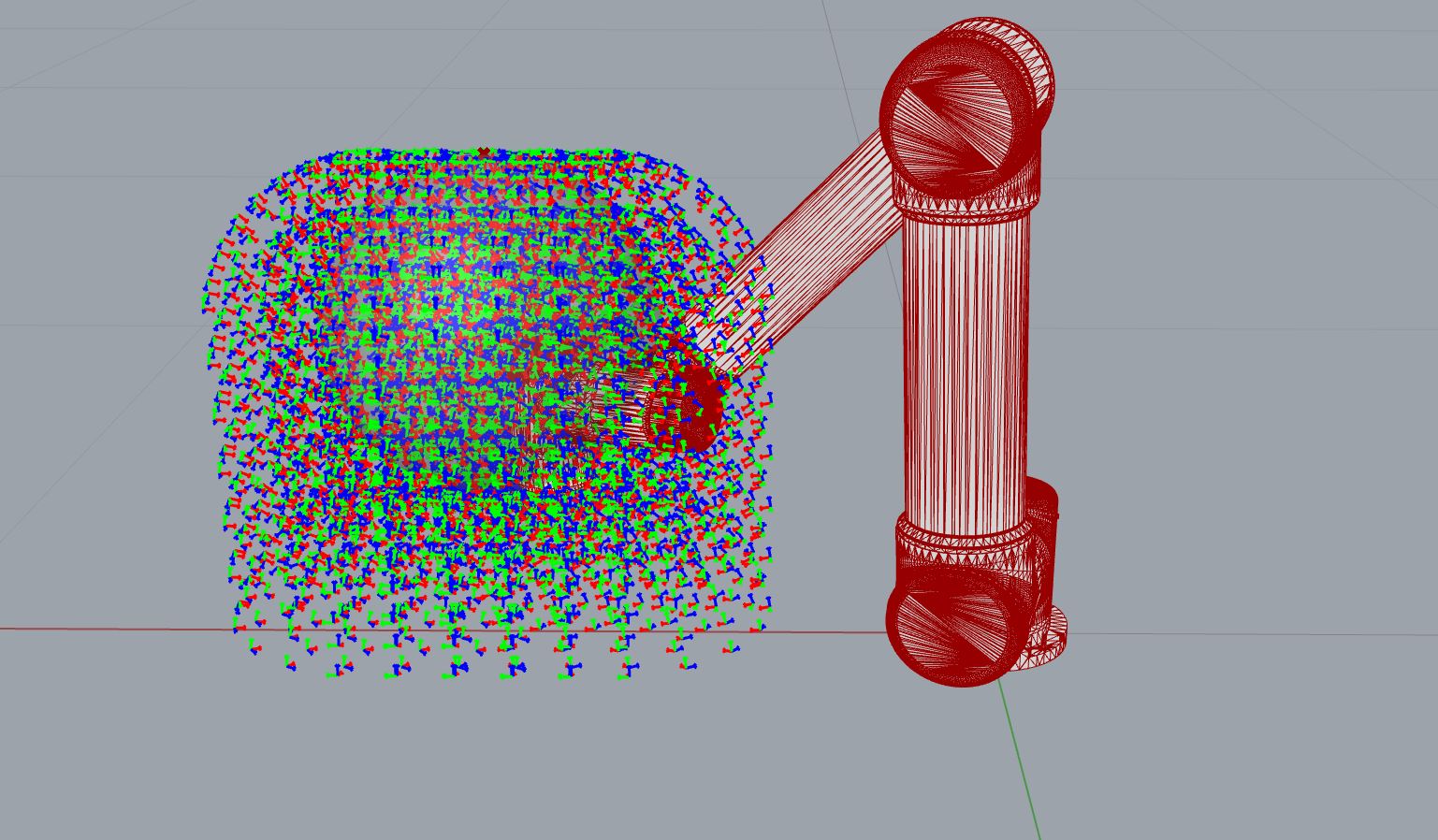
In this case, we actually evaluate 5705 (= 35 x 163) frames, see figure below.
We can easily check the shape of the reachability as follows:
>>> map.shape
(35, 163)
Visualizing the results in Rhino/GH gives an indication of the best position for the tested spheres. The score ranges now from 436 to 937. We can ask the map for the best score, returning the score and the index:
>>> map.best_score
(937, 20)
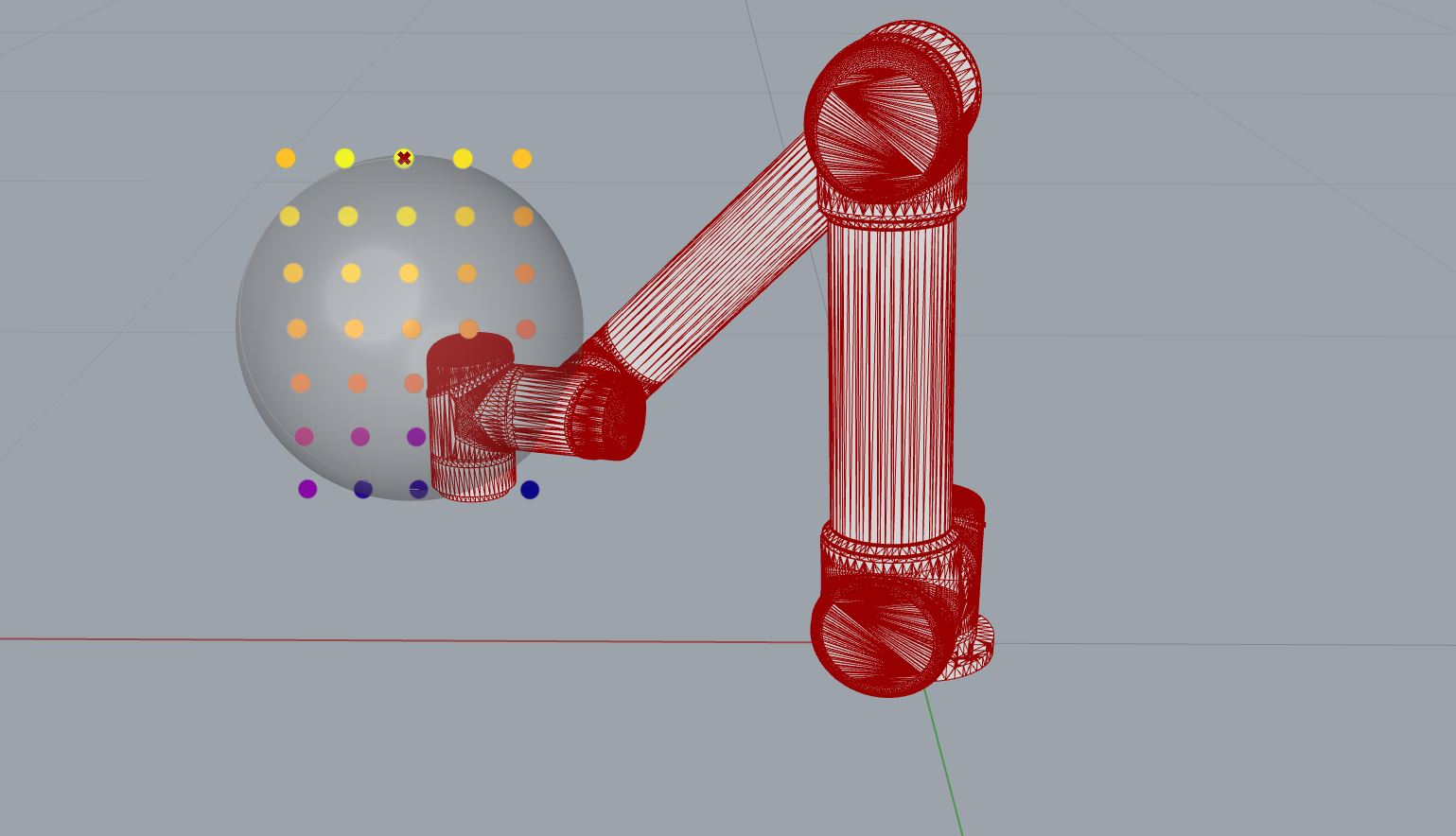
Note
Please note that the points of the point cloud correspond to the first frame
point of each of the 2D lists and NOT the sphere center. This can however be
changed by passing the sphere_centers for the artist to override.
>>> points, colors = artist.draw(points=sphere_centers)